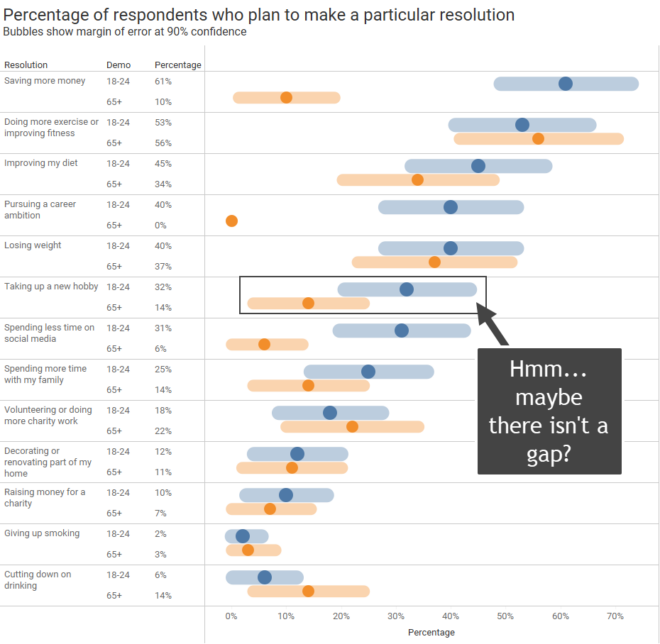
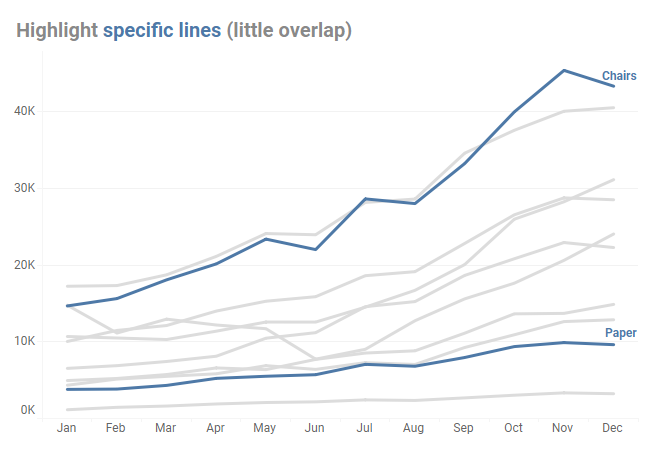
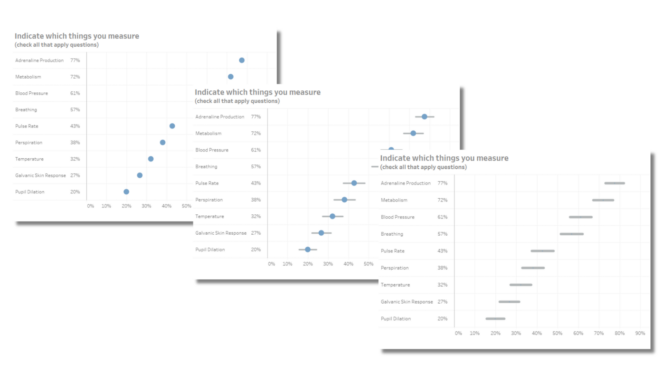
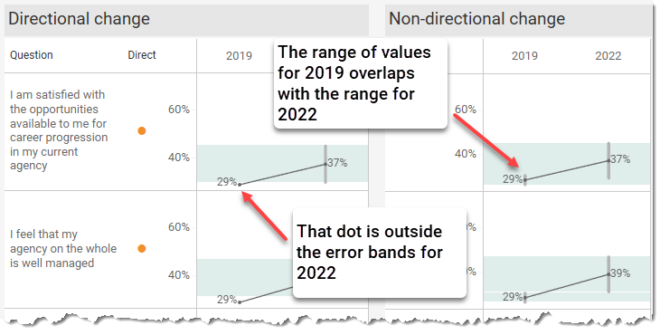
Just how carefully did you look at the data?
Delight, dismay, and why it’s your responsibility to vet the data Thank you to Alli Torban, Anna Foard, and Ben Jones for their feedback. My Delight A few weeks ago, I saw this terrific interactive graphic in one of my social media feeds. It was part of a recent Makeover Monday challenge. What a great [...]